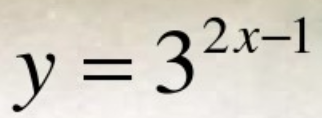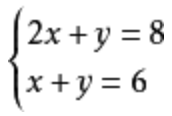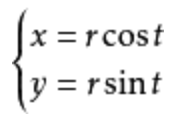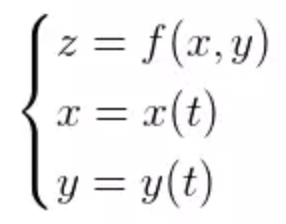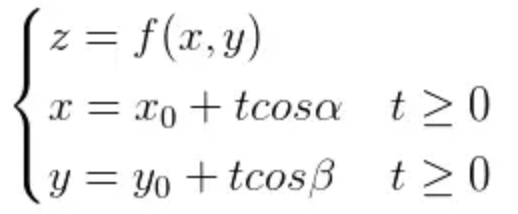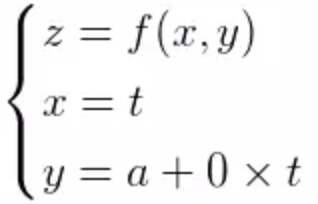微积分 & 概率统计 & 机器学习 & 深度学习 & 神经网络 相关概念
数
数轴上的点对应的数称为实数。实数分两类,有理数和无理数。
有理数是两个整数的比,结果可能是整数、或者分数。
小数是实数的一种表现形式。整数部分为0的称为纯小数,整数部分不为0的称为带小数。
从定义上讲,有理数=分数=小数,只是表现形式不同。其实整数是分母为1的分数。所有分数也是两个整数的比,但是通常我们把比值不为整数的才称为分数,把带小数点的才称为小数。
无理数是小数部分为无限不循环的数值。比如π。
大于等于0的整数称为自然数。
固定不变的数称为常数,比如1、2、π等
平面上的点称为复数。通常用a+bi表示一个复数,其中a称为实部、b称为虚部,i称为虚部单位。
当虚部为0时,复数即为实数。当实部为0、虚部不为0时,称为纯虚数。
复数跟平面向量一一对应
我们为了适应自然数加法的逆运算减法,扩展了自然数,定义了整数
我们为了整数乘法的逆运算除法,我们扩展了整数,定义了分数
我们为了负数的平方根,扩展了实数,定义了虚数。
函数
函数是一堆有序的事物对,事物可以是数字也可以是任何其他东西,并且事物对的第一个位的每个成员都跟其他成员不同。
比如:[{1,a},{2,a},{3,b}]。该函数由三个事物对组成,事物对的第一个位由1,2,3组成,每个成员都跟其他成员不同。
事物对的第一位组成的集合称为定义域,事物对的第二位组成的集合称为值域,第一位跟第二位的映射关系称为公式或者法则。
在方程y=f(x),x称为自变量,y称为因变量。自变量需要人为赋值,因变量由自变量根据公式自动计算得出。
只包含一个自变量的方程称为一元函数,表示为y=f(x),只包含两个自变量的方程称为二元函数,表示为y=f(x1,x2),以此类推。
由字母和数字组成的代数式称为单项式,如x²,2x。一个字母或一个数字也称为单项式。
有多个单项式相加组成的代数式称为多项式,如1+2、2x-3y。减法相当于加相反数。多项式中的每个单项式称为多项式的项。多项式中不含字母的项称为常数项。
这些单项式中的最高次数定义为这个多项式的次数。比如x+1是一次多项式。x²+1是二次多项式、一次类推。
形如f(x)=an·x^n+an-1·x^(n-1)+…+a2·x^2+a1·x+a0的函数,叫做多项式函数。当n=1时称为一次函数,n=2时称为二次函数,以此类推。
格式如f(x)=ax+b的一次函数称为线性函数,其中a和b为常数。线性函数在图像上表现为一条直线。
一次函数不等于线程函数,比如f(x)=sinx是一次函数,但不是线性函数。线性函数是一次函数的一种,一次函数包含线性函数。
对于函数f(x)的定义域I内的某个区间D上的任意两个自变量的值x1,x2:当x1<x2,则f(x1) < f(x2),则f(x)在区间D上是增函数;当x1>x2,则f(x1) > f(x2),则f(x)在区间D上是减函数。若函数y=f(x)在某个区间是增函数或减函数,则说函数(fx)在这个区间具有单调性,这个区间叫做函数f(x)的单调区间。
复合函数简单讲就是函数套函数,自变量也是函数的函数。比如:y=f(x), z=g(y),则z=f(g(x))就是一个符合函数,其中x是自变量,y是中间变量,x是因变量。复合函数的一个例子:
方程
含有等号的式子叫等式。如: 1+1=2、a+b=c。
方程是指含有未知数的等式。如:1+x=5。
使等式成立的未知数的值称为方程的解。
求方程的解的过程称为解方程。
方程组是将两个及以上的方程的组合在一起,使其中的未知数同时满足每个方程。如:
用于描述因变量和自变量关系的多个函数组成参数方程。通常我们用参数方程描述空间形状,如原的参数方程:
向量
向量指有大小和方向的量,可以表示为有箭头的线段,箭头代表方向,长度代表大小。有大小没方向的量叫标量。在物理学和工程学中,几何向量更常被称为矢量。
矩阵
矩阵是按照长方阵列排列的数的集合。
数组
所谓数组,是有序元素的序列,是计算机学科使用的一种数的表现方式。矢量也可以用一维数组表示,矩阵可以用二维数组表示。
坐标系
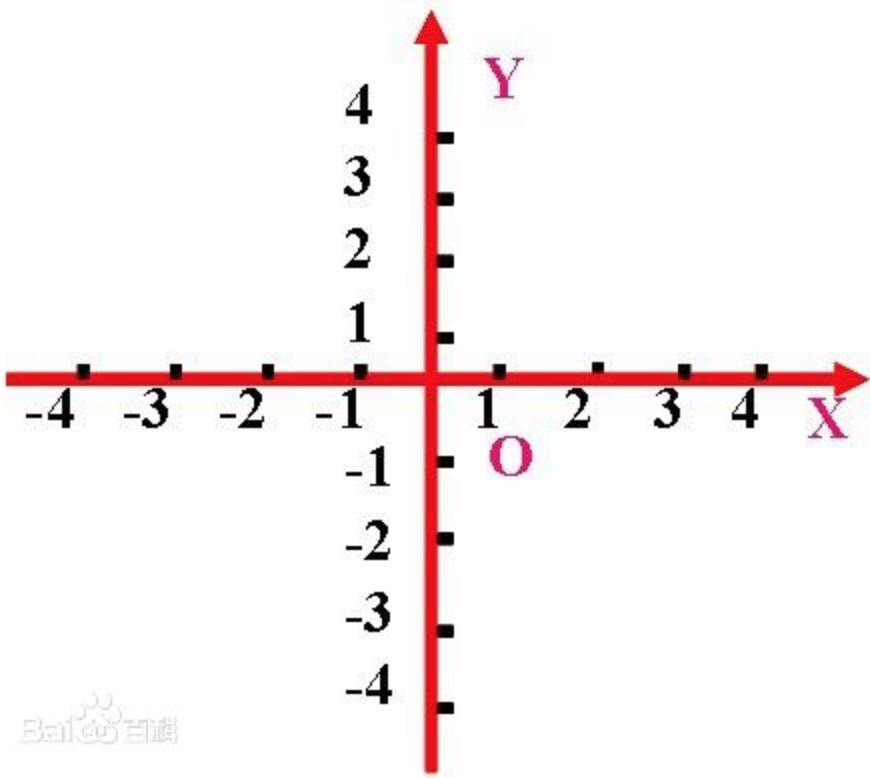
在平面内画两条互相垂直,并且有公共原点的数轴。其中横轴为X轴,纵轴为Y轴。这样我们就说在平面上建立了平面直角坐标系,简称直角坐标系。如图:
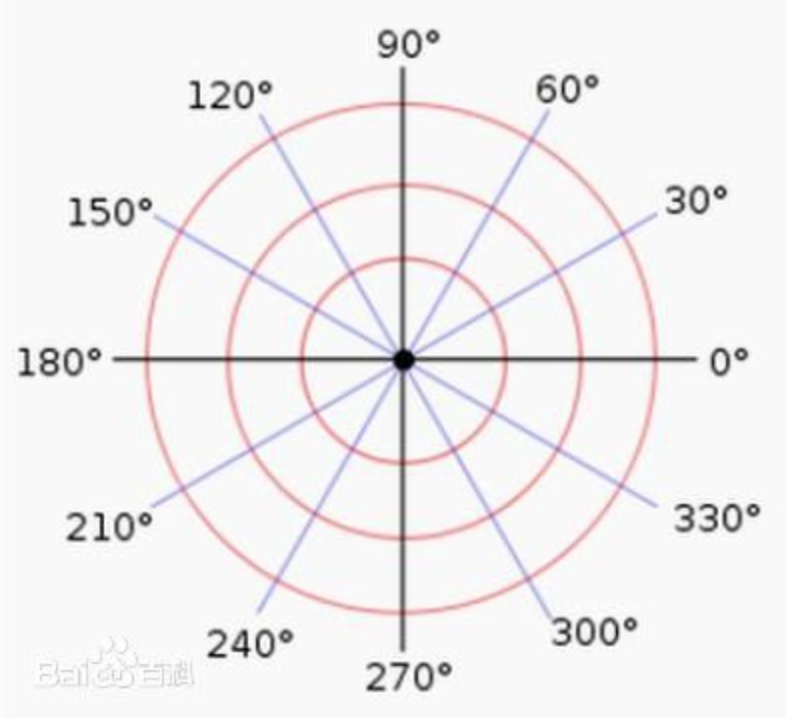
在平面上取一定点o,称为极点,由o出发的一条射线ox,称为极轴。再取定一个长度单位,通常规定角度取逆时针方向为正。这样,平面上任一点P的位置就可以用线段OP的长度ρ以及从Ox到OP的角度θ极坐标系极坐标系来确定,有序数对(ρ,θ)就称为P点的极坐标,记为P(ρ,θ);ρ称为P点的极径,θ称为P点的极角。如图:
导数
当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记做f’(x0)。
导数公式:
一个函数在某一点的导数描述了这个函数在这一点附近的变化率。
如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。
对于可导的函数f(x),x↦f’(x)也是一个函数,称作f(x)的导函数(简称导数)。寻找已知的函数在某点的导数或其导函数的过程称为求导。
方向导数指在函数定义域的内点,对某一方向求导得到的导数。通常函数为二次或三次函数。
函数的导数也叫一阶导数,对函数的导数再求导,则是二阶导数,即函数的导数的导数叫函数的二阶导数。
偏导数指在多元函数定义域的的内点,只对某个自变量的导数而保持其他自变量恒定不变。
关于全导数、方向导数、偏导数的一篇介绍:https://my.oschina.net/u/3053883/blog/1934604
全导数的参数方程:
方向导数的参数方程:
偏导数的参数方程:
概率统计
随机试验(random experiment)是在相同条件下对某随机现象进行的大量重复观测。随机试验的特点:1. 实验前不能确定将发生什么,但可以确定实验的全部结果是什么;2. 在相同条件下可以大量重复; 3. 实验结果是已随机方式或偶然方式出现。
随机事件是在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件(简称事件)。
随机试验中的每一个可能出现的试验结果称为这个试验的一个样本点,记作ωi。全体样本点组成的集合称为这个试验的样本空间。
在抛掷一枚均匀硬币的试验中,“正面向上”是一个随机事件。
梯度
函数上的某个点在各个自变量增长方向上的偏导数向量之和称为这个点的梯度。
对于一元函数,某个点的梯度就是该点的导数。
对于二元函数,某个的点的梯度是改点在x轴上的偏导数+改点在y轴上的偏导数。
函数在梯度方向上的变化率最快。
一篇形象介绍梯度的文章:《对“偏导数”和“梯度”最形象直观的解释》
机器学习
机器学习方法是计算机利用已有的数据(经验),得出了某种模型(迟到的规律),并利用此模型预测未来(是否迟到)的一种方法。
所谓模型,指的是一套计算公式,及其公式的参数。
计算模型的算法很多,比较有名的有回归算法、神经网络算法、SVM(支持向量机)算法、推荐算法等。除此之外还有朴素贝叶斯算法、决策树算法等。
按照标签的有无,又分为监督学习算法和无监督学习算法,还有两者都不是的。监督学习算法会给出正确答案,无监督学习算法不会给出正确答案。线性回归、逻辑回归、神经网络、SVM都属于监督学习算法。推荐算法既不是监督学习算法也不是无监督学习算法。
神经网络发展到多个隐藏层的情况称为深度学习算法。
深度学习是机器学习的子类,机器学习优势人工智能的子类。
需要保持一个信念:所有的计算问题都可以通过方程式求解。
神经网络
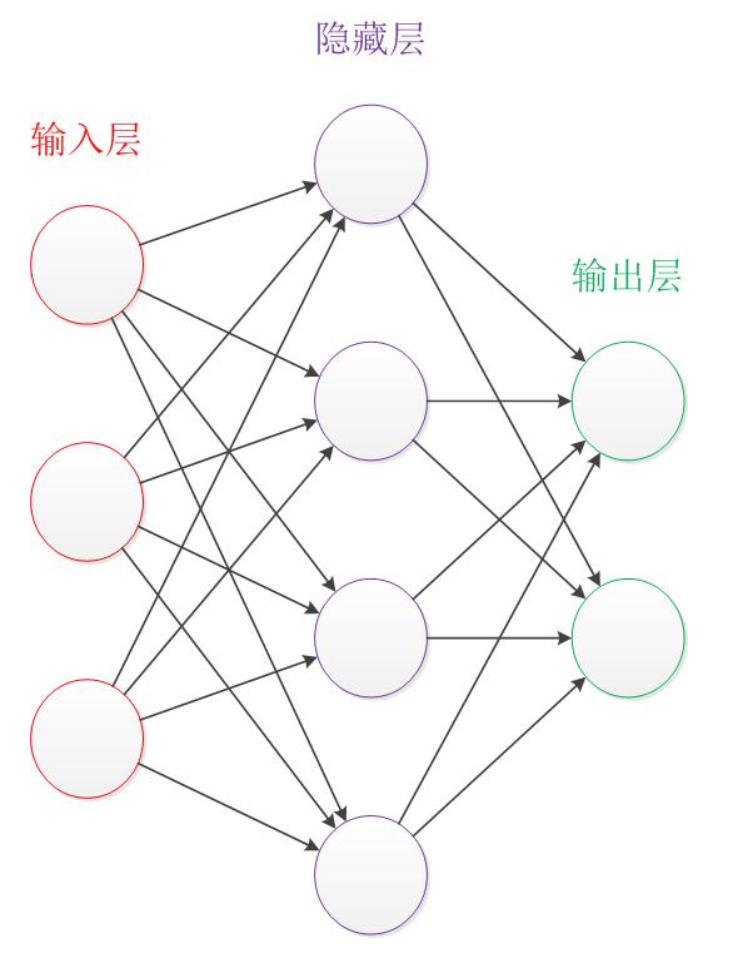
一个典型的神经网络包含三个层次,第一层为输入层,第二次为中间层,也叫隐藏层,第三层是输出层。
一般输入层和输出层的节点数是固定的。
神经网络结构图中的拓扑与箭头代表预测时的数据流向,跟训练时的数据流向有一定区别。
圆圈代表神经元,每个连接线代表一个关联关系和权重。网络结构是预先设计好的,而权重这是训练要得到的。
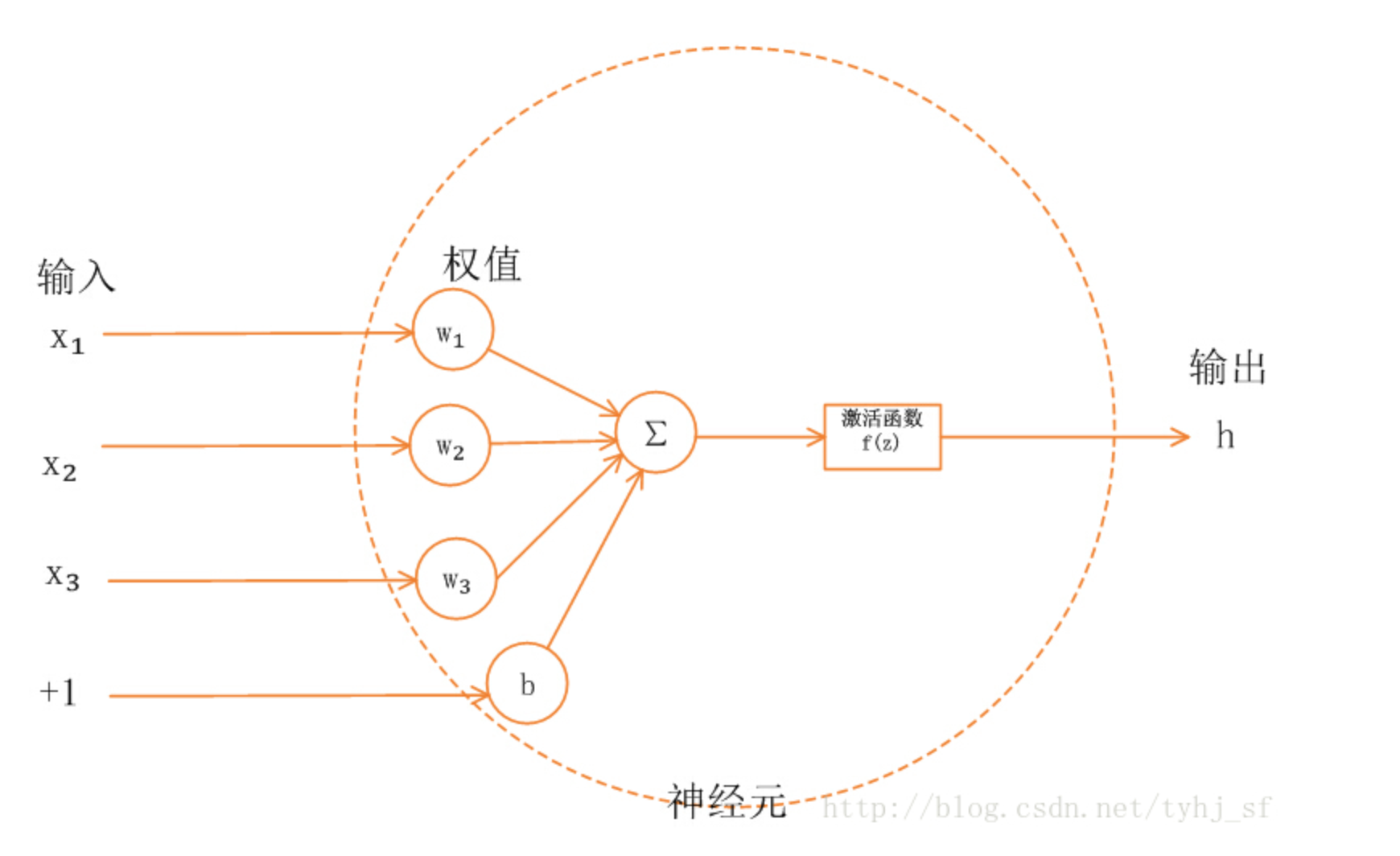
神经元节点模型:
x代表输入,可能有多个输入。w代表每个输入的权重,b为截距,通常为常量,sum表示将多个权重求和。sgn是激活函数。z是节点输出。
激活函数通常是非线性函数。为什么要用激活函数呢?如果没有激活函数,则输出是输入的线性组合,这跟没有隐藏层的效果相当,网络逼近能力就很有限,而是用非线性函数可以大幅增强网络表达能力,可以逼近任意函数,可以更好的拟合目标函数。常用的的激活函数由sigmoid、reLU等,各自的优缺点自行搜索吧。
通常会随机初始化输入值,使用这些随机值和模型预测样本,假设预测出来的值为output,真实的值是target,则target和output的误差称为损失函数(loss function)也称为代价函数(cost function)。
通常我们这样定义损失函数:
模型训练的目标就是让损失函数最小。而常用的方法就是求导,但是由于参数较多,计算导数为0的计算量太大,所有通常使用梯度下降算法,及每次计算当前参数的梯度,然后然参数沿着梯度的反方向移动一小段距离后再计算梯度,知道梯度最小。由于神经网咯结构复杂,计算梯度通常采用反向传播算法,具体可以看这边文章:《一文弄懂神经网络中的反向传播法——BackPropagation》。
参考
神经网络基本概念和流程:https://blog.csdn.net/u014162133/article/details/81181194
神经网络发展史:https://blog.csdn.net/illikang/article/details/82019945